Practice taking celestial sights while landlocked by using an artificial horizon

There are many references and books explaining how to reduce the sextant altitude to a usable fix. As I perused the various books and references it became clear to me that all were focused on the reduction of the sight and not to the methods or techniques of getting the sextant altitude in the first place.

Gaining proficiency in getting an accurate altitude, in my opinion, is the first and most important step in celestial navigation and the only way to get proficient is to practice. When not on the ocean for the perfect horizon, the next best option is to use an artificial horizon from your backyard. If the sky is clear and the sun, moon, planets or stars are visible then get out there and practice.

What is an artificial horizon? Basically it is a flat, level, horizontal, reflecting surface. A small pan filled with oil or water will work just fine. You only need to be certain that the surface of the liquid is not disturbed in any way while taking the sight. I use a Davis Instrument Artificial Horizon, which, as you can see in Figure 1, is a simple design complete with glass plates closing the unit off from any air disturbances. It costs about $27 and comes with colored plastic filter panes that can be used to diminish the intensity of the sun. An alternative to the artificial horizon is to use a practice horizon bubble, which attaches directly to the sextant. Celestaire, www.celestaire.com, offers both bubble horizons and the Davis Artificial Horizon.
One drawback to the design of the sloped frame glass plate holder is that the water used will evaporate and could condense on the inside of the glass plates. This should be wiped clean before your sight is made.

The artificial horizon can be used with any celestial object bright enough to be reflected off of the artificial horizon's liquid surface. Fill the bottom of the artificial horizon with water and then position it toward the object of interest, in this case the sun. Use the shadow cast by the artificial horizon as an indication when it is pointed in the direction of the object, as seen in Figure 2.

Notice that the sun's image in Figure 2 is not very stable. You have to wait until in settles down before you would take a sight. Once you have a stable reflection on the liquid surface of the artificial horizon you are ready to measure the altitude of the object. I use a Davis Mark 3 plastic sextant for my practice sessions.

With the sun's image reflecting from the stable artificial horizon, align the sight tube of the sextant to the sun in the sky. Your index should be set to 0 degrees when you do this. If you have no index error the sun should be in the center of the sight tube and an image of the sun will be on the index arm mirror. It is this image in the index arm mirror you will bring down to the sun's reflected image off of the artificial horizon's
liquid surface.

Keeping the sun's reflection in mind, bring the sun's image in the index mirror down to the sun's reflection. At this time, bring the index image over the artificial horizon's image so that one is on top of the other and take the time this is done. Since it is not possible to see both images coincide, use a gentle pendulum motion, swinging the index image over the reflected image, and when it seems that both are at the same place that is when you record the time of the sight and the angle from the sextant.

Figure 3 shows both the reflected sun from the artificial horizon's surface (in blue) and the index mirror reflection (in red). Notice that the index image is too low and must be moved up slightly to be equal with the reflected image.

The next step is to read the angle from the sextant. Keep in mind that the angle recorded by the sextant is twice the actual angle of the altitude of the sun. All angles measured with the artificial horizon are always twice the angle of the altitude of the object. The sextant is not level when you take a sight with the artificial horizon. You are actually looking down on the artificial horizon's liquid surface reflection of the sun at the same angle of the sun's actual altitude (see Figure 4). Hence, when you bring the sun's image down to the artificial horizon's liquid surface the index arm moves twice the altitude angle.

The use of an artificial horizon is limited to a sighting of an object that is less than about 50 degrees actual altitude because your scale on the sextant is only able to measure angles less than 100 degrees; 50 degrees times two equals 100 degrees on your scale. The artificial horizon works best well before the meridian crossing or well after the meridian crossing of an object.

If you use this method and bring the two reflected images in coincidence (one on top of the other) you do not have to worry about making the semi-diameter corrections since the images in coincidence are centered on the sun's (or moon's) center and not either limb. The dip correction is not needed because you are not above the natural horizon. As you recall, the higher up your eye is when you take the sight the farther away the horizon is. This adds an error that must be corrected for when using the natural horizon, but not with an artificial horizon. You only have to include the index error and refraction or parallax errors if applicable. These errors are either indicated in the tables you use or the computer program will determine those corrections for you.

Since this article is about using an artificial horizon in order to get lots of practice using your sextant, I suggest using a computer program to do the reductions for you. This allows you to take many sights using the sun, moon planets or navigation stars.

The program I use to reduce the sight data is Navigator by Omar Reis, Version 2006. As an example of how the technique works, I will use actual data I collected with my sextant and artificial horizon from my backyard in Tucson, Arizona, and reduce that data for a fix using the Navigator software.

I used the moon and the planet Jupiter, which were both nicely placed on the evening sky of July 14, 2008. The configuration in the sky is seen in Figure 5. Jupiter is the bright dot to the left of center and the moon is the very obvious bright object to the right and above Jupiter. The image of the moon is reflected from the artificial horizon as can be easily seen in Figure 6.

The index mirror image of the moon is brought down to the reflected image. When the images coincided the time was taken and angle recorded. The actual data are as follows.

For the moon:
" The local time was 09:07:34 MST July 14, 2008 (04:07:34 July 15, 2008 UTC)
" The angle measured was 56 degrees and 52 minutes (the actual double angle).
" The index error was 0 degrees.
" The watch correction was +5 seconds.

For Jupiter:
" The local time was 09:04:44 MST (04:04:44 UTC)
" The angle measured was 41 degrees and 22 minutes (the actual double angle).
" The index error was 0 degrees.
" The watch correction was +5 seconds.
The Navigator program has an artificial horizon mode and you enter the sextant reading exactly as recorded on the sextant. The program then divides the angle by two and does not apply the semi-diameter correction for the moon (or sun) and does not apply the dip correction. It does correct for parallax as well as refraction, if applicable. You input the data and then have Navigator plot the LOPs and compute a fix, as seen in Figure 7.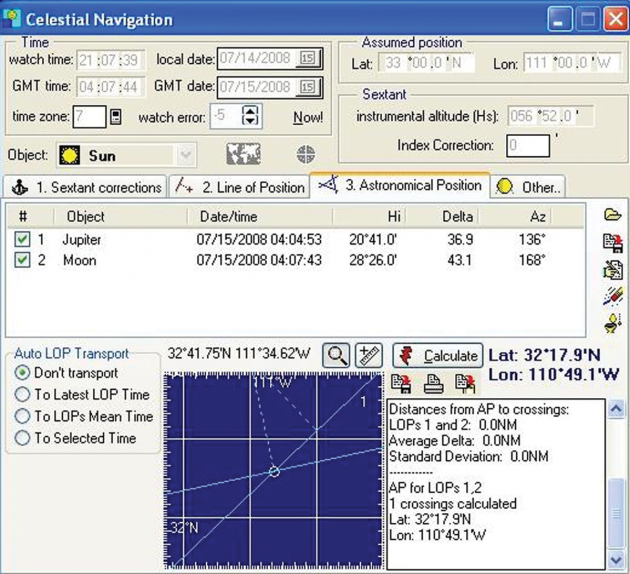

In this case it computed the following: Latitude 32 degrees, 17.9 minutes North, Longitude 110 degrees, 49.1 minutes West.

How good is the fix? To find out, take the fix as calculated by the program and input the latitude and longitude into an online mapping program-I used Google Maps-and see how close you are to the place from which you took your sight. The calculated position, determined from my Jupiter and moon sights, is plotted on the map as "A" and labeled "Fix", and the location from which I took the sight is labeled "Actual." The map in Figure 8 shows both points. The error from my actual position compared with the sextant-reduced fix is slightly more than a mile. That is an acceptable error using the equipment described. Not bad at all!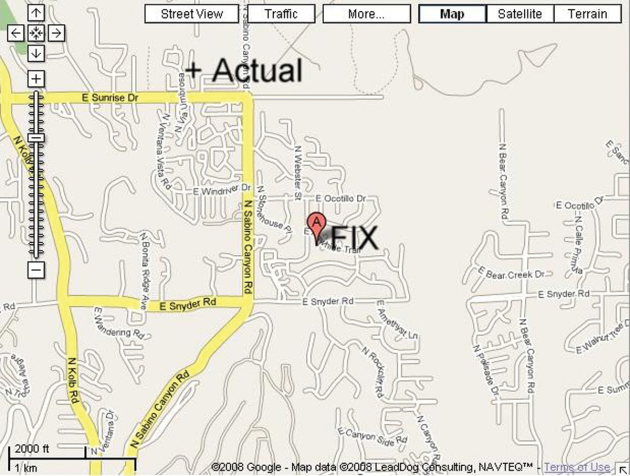

David G. Iadevaia is a professor of astronomy and physics in Tucson, Arizona. When not doing science or writing he can be found sailing out of San Diego on his 1983 Catalina 36 Principessa.